Capacitance values
Finally, we can look at how the size and construction of capacitors affects their capacitance. The capacitance of a basic capacitor for example, consisting of two parallel, flat plates separated by a dielectric may be calculated from the formula:
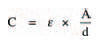
where ε is the permittivity of the dielectric, A is the area of overlap of the plates, and d is the distance between the plates.
Different insulating materials have different permittivities, so different capacitor values may be made, simply by using different dielectrics. Air, say, has a permittivity of about 9 x 10-12 farads per metre (that is, 9 x 10-12 Fm-1). Permittivities of other materials are usually expressed as a relative permittivity, where a material’s relative permittivity is the number of times its permittivity is greater than air. So, for example, mica (a typical capacitor dielectric), which has a relative permittivity of 6, has an actual permittivity of 54 x 10-12 Fm-1 (that is, 6 x 9 x 10-12 Fm-1).
So, a possible capacitor, consisting of two parallel metal plates of overlapping area 20 cm2, 10 mm apart, with a mica dielectric, has a capacitance of:
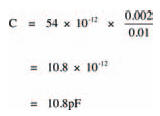
Er, I think that’s enough theory to be grappling with for now, don’t you? Try your understanding of capacitors and how they work with the chapter’s quiz.
<< Theoretical aspects