Theoretical aspects
So what is it about a capacitor which causes this delay in voltage between switching on or off the electricity supply and obtaining the final voltage across it? It’s almost as if there’s some mystical time delay inside the capacitor. To find the answer we’ll have to consider a capacitor’s innards again.
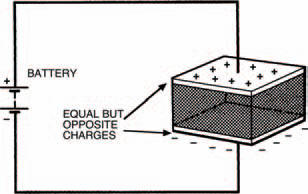
Figure 4.15 This is the capacitor shown in Figure 4.1, but this time connected to a battery with opposite charges built up on each plate
Figure 4.15 shows the capacitor we first saw in Figure 4.1, but this time it is shown connected to a battery which, as we know, is capable of supplying electrons from its negative terminal. A number of electrons gather on the capacitor plate connected to the battery’s negative terminal, which in turn repel any electrons on the other plate towards the battery’s positive terminal. A deficiency in electrons causes molecules of this capacitor plate to have a positive charge, so the two plates of the capacitor now have equal, but opposite, electric charges on them.
Current only flows during the time when the charges are building up on the capacitor plates — not before and not after. It’s also important to remember that current cannot flow through the capacitor — a layer of insulator (known correctly as the dielectric) lies between the plates, remember — current only flows in the circuit around the capacitor.
If we now completely disconnect the charged capacitor from the battery, the equal and opposite charges remain — in theory — indefinitely. In practice, on the other hand, charge is always lost due to leakage current between the plates. You can try this for yourself, if you like: put a capacitor into the breadboard then charge it up by connecting the battery directly across it. Now disconnect the battery and leave the capacitor in the breadboard for a time (overnight, say). Then connect your meter across it to measure the voltage. You should still get a reading, but remember that the resistance of the meter itself will always drain the charge stored.
The size of the charge stored in a capacitor depends on two factors; the capacitor’s capacitance (in farads) and the applied voltage. The relationship is given by:
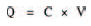
where Q is the charge measured in coulombs, C is the capacitance and V is the voltage. From this we can see that a charge of one coulomb is stored by a capacitor of one farad, when a voltage of one volt is applied.
Alternatively, we may define the farad (as we promised we would, earlier in the chapter) as being the capacitance which will store a charge of one coulomb when a voltage of one volt is applied.
We can now understand why it is that changing the capacitor value changes the time constant, and hence changes the associated time delay in the changing voltage across the capacitor. Increasing the capacitance, say, increases the charge stored. As the current flowing is determined by the resistance in the circuit, and is thus fixed at any particular voltage, this increased charge takes longer to build up or longer to decay away. Reducing the capacitance reduces the charge, which is therefore more quickly stored or more quickly discharged.
Similarly, as the resistor in the circuit defines the current flowing to charge or discharge the capacitor, increasing or decreasing its value must decrease or increase the current, therefore increasing or decreasing the time taken to charge or discharge the capacitor. This is why the circuit’s time constant is a product of both capacitance and resistance values.
<< The other way