Relationships
You’d be right in thinking that there must be some form of relationship between this pushing power in volts and the rate of electron flow in amps. After all, the higher the voltage, the more pushing power the electrons have behind them so the faster they should flow. The relationship was first discovered by a scientist called Ohm, and so is commonly known as Ohm’s law. It may be summarised by the expression:
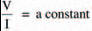
where the constant depends on the substance through which the current flows and the voltage is applied across. Figure 1.5 gives an example of a substance which is connected to a cell. The cell has a voltage of 2 V, so the voltage applied across the substance is also 2 V. The current through the substance is, in this case, 0.4 A. This means, from Ohm’s law, that the constant for the substance is:
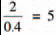
The constant is commonly called the substance’s resistance (because it is, in fact a measure of the amount the substance resists the flow of current through it) and is given the unit: Ω (pronounced ohm — not omega — after the scientist, not the Greek letter its symbol is borrowed from). So, in our example of Figure 1.5, the resistance of the substance is 5 Ω. In some literature the letter R is used instead of Ω. Different substances may have different resistances and may therefore change the current flowing.
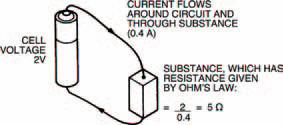
Figure 1.5 Cell’s voltage is 2 V, and a current of 0.4 A flows
Take note: This is a vitally important concept — probably the most important one in the whole world of electronics — and yet it is often misunderstood. Even if it is not misunderstood, it is often misinterpreted.
Indeed, this is so important, let’s recap it and see what it all means: If a voltage (V — measured in volts) is applied across a resistance (R — measured in ohms), a current (I — measured in amps) will flow. The voltage, current and resistance are related by the expression (1):
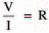 (1)
(1)
The importance of this is that the current which flows depends entirely on the values of the resistance and the voltage. The value of the current may be determined simply by rearranging expression 1, so that it gives (2):
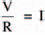 (2)
(2)
So, a voltage of say 10 V, applied across a resistance of 20 Ω, produces a current of:
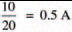
Similarly, if we have a resistance, and a current is made to flow through it, then a voltage is produced across it. The value of the voltage may be determined by again rearranging expression 1, so that it now gives (3):
 (3)
(3)
Hint: Ohm’s law
A simple method to help you remember Ohm’s law: remember a triangle, divided into three parts. Voltage (V) is at the top. Current (I) and resistance (R) are at the bottom: it doesn’t matter which way round I and R are – the important thing to remember is V at the top. Then, if you have any two of the constants, cover up the missing one with your finger and the formula for calculating the missing one will appear. Say you know the voltage across a resistor and the current through it, but you need to know the resistance itself. Simply cover the letter R with your finger:
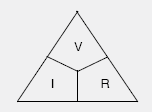
and the formula to calculate the resistance is then given as: V/I
Thus, a current of, say, 1 A flowing through a resistance of 5 Ω, produces a voltage of:

across the resistance.
These three expressions which combine to make Ohm’s law are the most common ones you’ll ever meet in electronics, so look at ’em, read ’em, use ’em, learn ’em, inwardly digest ’em — just don’t forget ’em. Right? Right.
Take note:
And another thing. See the way we’ve said throughout, that a voltage is applied or produced across a resistance. Similarly a current flows through a resistance. Well let’s keep it like that! Huh? Just remember that a voltage is across: a voltage does not flow through. Likewise, a current flows through: it is not across.
There is no such thing as a flow of voltage through a resistance, and there’s no such thing as a current across a resistance.
<< Ideas about electricity