Ouch, that hertz
We can calculate the rate at which the LED flashes, more accurately, from formulae relating to the 555. A quick study of the square wave output shows that it consists of a higher voltage for a time (which we can call T1) and a lower voltage for a time (which we will call T2).
Now, T1 is given by:
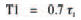
and T2 is given by:
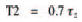
So, the time for the whole period of the square wave is:
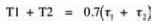
and as the frequency of a waveform is the inverse of its period we may calculate the waveform’s frequency as:
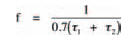
Earlier, we defined the two time constants, τ1 and τ2, as functions of the capacitor and the two resistors, and so by substituting them into the above formula, we can calculate the frequency as:
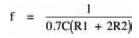
So, the frequency of the output signal of the circuit of Figure 5.2 is:
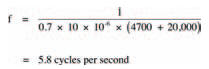
or, more correctly speaking:

Equation 1 is quite important really, because it shows that the frequency of the signal is inversely proportional to the capacitance. If we decrease the value of the capacitor we will increase the frequency. We can test this by taking out the 10 μF capacitor and putting in a 1 μF capacitor. Now, the LED flashes so quickly (about 58 times a second) that your eye can’t even detect it is flashing and it appears to be always on. If you replace the capacitor with one of a value of say 100 μF the LED will flash only very slowly.
Now, let’s stop and think about what we’ve just done. Basically we’ve used a capacitor in precisely the ways we looked at last chapter — to charge and discharge with electrical energy so that the voltage across the capacitor goes up and down at the same time. True, in the experiments last chapter you were the switch, whereas this chapter an IC has taken your place. But the principle — charging and discharging a capacitor — is the same.
The current which enters the capacitor to charge it, then leaves the capacitor to discharge it, is direct current because it comes from a 9 V d.c. battery. However, if we look at the output signal (Figure 5.3(c)) we can see that the signal alternates between two levels. Looked at in this way, the astable multi-vibrator is a d.c.-to-a.c.converter. And that is going to be useful in our next experiment, where we look at the way capacitors are affected by a.c. The circuit we shall look at is shown in Figure 5.5 and is very simple, but it’ll do nicely, thank you. It should remind you of a similar circuit we have already looked at; the voltage divider, only one of the two resistors of the voltage divider has been replaced by a capacitor. Like an ordinary voltage divider the circuit has an input and an output. What we’re going to attempt to do in the experiment is to measure the output signal when the input signal is supplied from our astable multivibrator.
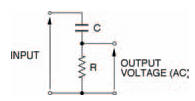
Figure 5.5 A voltage divider — but with a capacitor
Figure 5.6 shows the whole circuit of the experiment while Figure 5.7 shows the breadboard layout. The procedure for the experiment is pretty straightforward: measure the output voltage of the a.c. voltage divider when a number of different frequencies are generated by the astable multi-vibrator, then tabulate and plot these results on a graph. Things really couldn’t be easier. Table 5.1 is the table to fill in as you obtain your results and Figure 5.8 is marked out in a suitable grid to plot your graph. To change the astable multivibrator’s frequency, it is only necessary to change capacitor Cl. Increasing it ten-fold decreases the frequency by a factor of ten; decreasing the capacitor value by ten increases the frequency ten-fold. Five different values of capacitor therefore give an adequate range of frequencies.
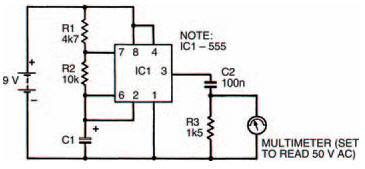
Figure 5.6 A circuit combining the astable multi-vibrator and the circuit in Figure 5.5
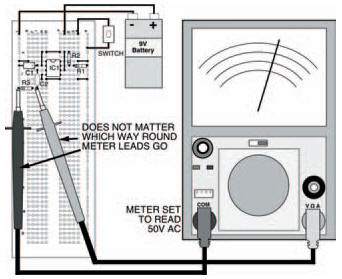
Figure 5.7 The breadboard layout of the circuit in Figure 5.6. It is the same as that in Figure 5.4, with a capacitor in place of the LED

Table 5.1 Results when capacitor C2 is 100 nF
Figure 5.8 A blank graph on which you can plot your experimental results. Use Table 5.1 above as well
As you do the experiment you’ll find that only quite low voltages are measured (up to about 4 V a.c.) so depending on your multi-meter’s lowest a.c. range you may not achieve the level of accuracy you would normally desire, but the results will be OK, nevertheless.
Table 5.2 and Figure 5.9 show my results which should be similar to yours (if not, you’re wrong — I can’t be wrong, can I?). The graph shows that the size of the output signal of the a.c. voltage divider is dependent on the frequency of the applied input signal. In particular, there are three clearly distinguishable sections to this graph, each relating to frequency.

Table 5.2 My tabled results
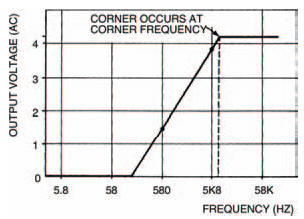
Figure 5.9 Graphed results of Table 5.2
First, above a certain frequency, known as the corner frequency, the output signal is constant and at its maximum.
Second, at low frequencies (close to 0 Hz) the output is zero.
Third, between these two sections the output signal varies in size depending on the applied input signal frequency.
Is this the same for all a.c. voltage dividers of the type shown in Figure 5.5? Well, let’s repeat the experiment using a different capacitor for C2, to find out.
Try a 10 nF capacitor and repeat the whole procedure, putting your results in Table 5.3 and Figure 5.10. Table 5.4 and Figure 5.11 show our results.

Table 5.3 Results when capacitor C2 is 10 nF
Figure 5.10 A graph for use with your results from the experiment with the 10 nF capacitor in Table 5.3
And yes, the graph is the same shape but is moved along the horizontal axis by an amount equivalent to a ten-fold increase in frequency (the capacitor was decreased in value by tenfold, remember). A similar inverse relationship is caused by changing the resistor value, too.
Frequency, capacitance and resistance are related in the a.c. voltage divider by the expression:
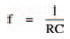
where f is the corner frequency. For the first voltage divider, with a capacitance of 10 nF and a resistance of 1.5 kΩ, the corner frequency is:
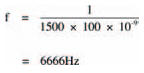

Table 5.4 My results (C2 = 10 nF)
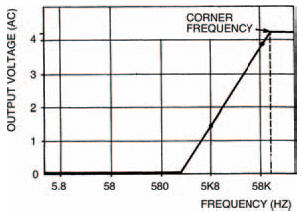
Figure 5.11 Graph of my results from Table 5.4 in the same experiment
which is more or less what we found in the experiment. In the second voltage divider, with a 10 nF capacitor, the corner frequency increases by ten to 66,666 Hz.
Remembering what we learned last chapter about resistors and capacitors in charging/discharging circuits, we can simplify the expression for corner frequency to:
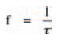
because the product RC is the time constant, τ. This may be easier for you to remember.
An a.c. voltage divider can be constructed in a different way, as shown in Figure 5.12. Here the resistor and capacitor are transposed. What do you think the result will be? Well, the output signal size now decreases with increasing frequency — exactly the opposite effect of the a.c. voltage divider of Figure 5.5! All other aspects are the same, however: there is a constant section below a corner frequency, and a section where the output signal is zero, as shown in Figure 5.13. Once again the corner frequency is given by the expression:
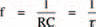
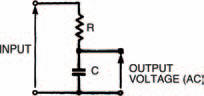
Figure 5.12 An a.c. voltage divider with the resistor and capacitor transposed
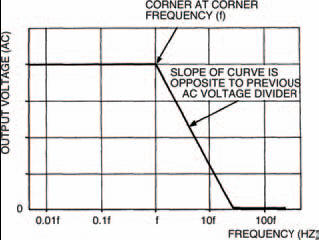
Figure 5.13 This graph shows the similarities and differences between this circuit and that in Figure 5.5
<< Throwing light on it