Maths
Although diodes are non-ohmic, this doesn’t mean that their operation can’t be explained mathematically (just as Ohm’s law or, V = IR, say is a mathematical formula). Diodes, in fact, follow a relationship every bit as mathematical as Ohm’s law. The relationship is:
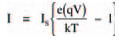
where I is the current through the diode, Is is the saturation reverse current, q is the magnitude of an electron’s charge, k is Boltzmann’s constant, and T is the absolute temperature in degrees Kelvin. As q and k are both constant and at room temperature the absolute temperature is more or less constant, the part of the equation q/kT is also more or less constant at about 40 (work it out yourself if you want: q is 1.6 x 10-19 C; k is 1.38 x 10-23 JK-1 and room temperature, say, 17°C is 290 K.
The equation is thus simplified to be approximately:
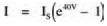
The exponential factor (e40V), of course confirms what we already knew to be true — that the diode characteristic curve is an exponential curve. From this characteristic equation we may calculate the current flowing through a diode for any given voltage across it, just as the formulae associated with Ohm’s law do the same for resistors.
Hint:
But even with this simplified approximation of the characteristic equation you can appreciate the value of having a characteristic curve in front of you to look at. If I had the option between having to use the equation or a diode characteristic curve to calculate the current through a diode, I know which I’d choose!
<< Diodes II